Final Answer:
The farmer picked oranges and distributed them equally into 9 boxes, resulting in each box containing the same number of oranges.
Explanation:
The farmer's task involved a fair distribution of oranges among 9 boxes, ensuring each box received an equal share of the harvest. To determine the number of oranges in each box, we can express this situation algebraically. Let O represent the total number of oranges and B represent the number of boxes. The equation for this scenario is
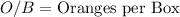 . Since the question specifies that each box had the same amount of oranges, we can further express this as
. Since the question specifies that each box had the same amount of oranges, we can further express this as
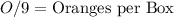 , where 9 is the number of boxes.
, where 9 is the number of boxes.
Now, for a more detailed explanation, consider if the farmer picked 81 oranges in total (9 boxes multiplied by the same number of oranges per box). The equation becomes 81/9 = 9. Thus, each box would contain 9 oranges. This demonstrates the equal distribution of the total harvest among the 9 boxes, ensuring fairness and consistency.
In conclusion, by dividing the total number of oranges by the number of boxes, we obtain the desired result: each box contains the same amount of oranges. This mathematical approach simplifies the farmer's task of organizing and distributing the harvest, maintaining uniformity among the boxes and ensuring an equitable distribution of the produce.