Answer:
A. √(e + 14)
Explanation:

separating the variables, we have
2ydy = (
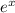 - 1)dx
- 1)dx
integrating, we have
∫ydy = ∫(
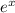 - 1)dx
- 1)dx
∫ydy = ∫
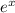 dx - ∫1dx + C
dx - ∫1dx + C
2y²/2 =
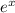 - x + C
- x + C
y² =
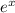 - x + C
- x + C
when x = 0, y = 4
So,
y² =
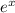 - x + C
- x + C
4² =
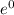 - 0 + C
- 0 + C
16 = 1 + C
16 = 1 + C
C = 16 - 1
C = 15
So,
y² =
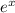 - x + 15
- x + 15
when x = 1, we find y
y² =
 - 1 + 15
- 1 + 15
y² = e + 14
y = √(e + 14)