Answer:
Inputting the values of x into f(x):
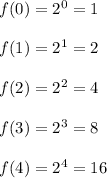
Comparing y-values of both functions:
f(x): 1, 2, 4, 8 , 16
g(x): -11, -10, -8, -4, 4
The difference between corresponding y-values of g(x) and f(x) is -12
Therefore, g(x) = f(x) - 12
If a new function h(x) is shifted by half as much, then h(x) = f(x) - 6
