Question

Hey could anyone help? Bit stuck on this question

Answer 1

Explanation:

You did it please don't delete

Answer 2

Some important concept before solving answer :-

`\\`

When ever there is three dimensional figure remember, where one figure is related to other then there's always relation with volume.

So it may get pretty difficult to understand therefore I am dividing into small parts for better understanding.

`\\`

`\pmb{ \bf \dag\cal{Part \ One:}}`

As we know there will be relation of volume, so let's find volume of the cone first.

`\\`

Given :-

⭑Height = 10 cm

⭑radius = 3cm

`\\`

To find :

⭑volume of cone

`\\`

Let represent :-

⭑Height as : h

⭑radius as : r

⭑volume of cone as : v

`\\ \\`

Formula to find volume of cone :-

`\\`

`\bigstar\boxed{ \rm v = \pi {r}^(2) * (h)/(3) }`

`\\`

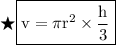
So let's find v!

`\\`

`\dashrightarrow\sf v = \pi {r}^(2) * (h)/(3)`

`\\ \\`

`\dashrightarrow\sf v = (22)/(7) * {3}^(2) * (10)/(3)`

`\\ \\`

`\dashrightarrow\sf v = (22)/(7) * {3} * 3* (10)/(3)`

`\\ \\`

`\dashrightarrow\sf v = (22)/(7) * {\cancel3} * 3* (10)/(\cancel3)`

`\\ \\`

`\dashrightarrow\sf v = (22)/(7)* 3* (10)/(1)`

`\\`

`\dashrightarrow\sf v = (22)/(7)* 3*10`

`\\ \\`

`\dashrightarrow\sf v = (22* 3*10)/(7)`

`\\ \\`

`\dashrightarrow\sf v = (22* 30)/(7)`

`\\ \\`

`\dashrightarrow\sf v = (660)/(7)`

`\\ \\`

`\dashrightarrow\bf v =94.3 {cm}^(3)`

`\\ \\`

`\pmb{ \bf \dag\cal{Part \: \: Two:}}`

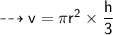
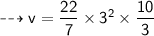
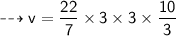
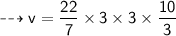
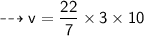
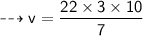
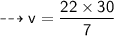
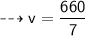
So remember that cone filled with water is equal to volume of cone.

volume of water filled in cone = volume of water in cuboid.

So you probably thinking that above sentence is wrong , cause they haven't told volumes of cuboid and cone are equal, but we have to find depth of water filled not depth of cuboid.

`\\ \\`

Given :-

⭑Volume of cuboid = 94.3 cm³

⭑Length of cuboid = 5cm

⭑Width of cuboid = 3cm

`\\`

To find :-

⭑Depth of water in cuboid

`\\`

Let represent:-

⭑Volume of cuboid as : V'

⭑Length of cuboid as : L

⭑Width of cuboid as : W

⭑Depth of water in cuboid as : D

`\\ \\`

Formula to find volume of cuboid :-

`\\ \\`

`\bigstar\boxed{ \rm V'= W * L * D }`

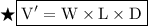
By using this formula we can find depth of cuboid.

`\\ \\`

`: \implies \sf V'= W * L * D`

`\\ \\`

`: \implies \sf 94.3= D * 3 * 5`

`\\ \\`

`: \implies \sf (943)/(10* 3 * 5) = D`

`\\ \\`

`: \implies \sf (943)/(10 * 15) = D`

`\\ \\`

`: \implies \sf (943)/(150) = D`

`\\ \\`

`: \implies \sf D = (943)/(150)`

`\\ \\`

`: \implies \bf D = 6.3cm`

`\\ \\`

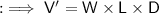
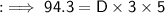
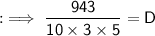
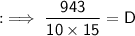
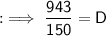
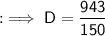
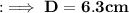
Required Answer:-

Depth = 6.3 cm