Question

What is an equation of the line that passes through the point(-1,-3) and is perpendicularly to the line x-2y=14

Answer 1

2x + y + 5 = 0

Explanation:

The equation of line is x-2y = 14 and we need to find the equⁿ of line which passes through (-1,-3) and is perpendicular to given line.

• Find the slope of given line by converting it into slope intercept form.

=> x - 2y = 14

=> 2y = x - 14

=> y = x-14/2

=> y = x/2 - 7

• Comparing to y = mx + c ,

=> Slope (m) = 1/2 .

Now the slope of line perpendicular to it , will have a slope ,

=>
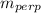`m_(perp)` = -1/m

=>
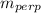`m_(perp)` = -1/½

=>
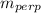`m_(perp)` = -2

• Using point slope form ,

=> m = (y - y₁) / ( x - x₁)

=> -2 = { y - (-3) } / { x - (-1) }

=> -2 = y + 3/x + 1

=> -2(x + 1) = y + 3

=> -2x -2 = y + 3

=> y + 2x +3+2 = 0

=> 2x + y + 5 = 0

Hence the equation of line perpendicular to it is 2x + y + 5 = 0 .

Answer 2

the equation will be

Explanation:

2x+y+5=0