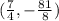Answer:
The y-intercept is y = -4.
The x-intercepts are
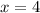 and
and
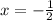
The vertex is
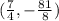
Explanation:
Quadratic equation:
Has the following format:
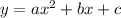
The y-intercept is c.
Finding the x-intercepts:
Given a second order polynomial expressed by the following equation:
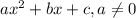 .
.
This polynomial has roots
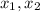 such that
such that
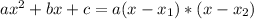 , given by the following formulas:
, given by the following formulas:
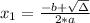
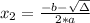
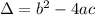
Vertex:
Suppose we have a quadratic function in the following format:
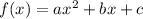
It's vertex is the point
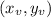
In which
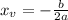
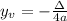
Where
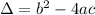
In this question:
The quadratic equation is
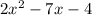 , which has
, which has
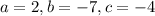 . This means that the y-intercept is y = -4.
. This means that the y-intercept is y = -4.
x-intercepts:
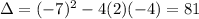
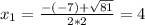
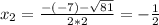
The x-intercepts are
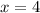 and
and
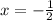
Vertex:
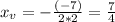
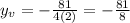
The vertex is