Given:
Angle A = 18.6°
Angle B = 93°
Length of side AB = 646 meters
To find:
the distance across the river, distance between BC
Steps:
Since we know the measure of 2 angles of a triangle we can find the measure of the third angle.
18.6° + 93° + ∠C = 180°
111.6° + ∠C = 180°
∠C = 180° - 111.6°
∠C = 68.4°
Therefore the measure of angle C is 68.4°.
now we can use the law of Sines,
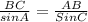
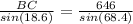
![BC[sin(68.4)] = 646 [sin(18.6)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/k41jvcn1cij7qq9ph4omwgnwd68wjh9rxz.png)


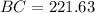
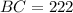 meters
meters
Therefore, the distance across the river is 222 meters.
Happy to help :)
If anyone need more help, feel free to ask