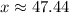Question

I still don’t understand this very well I don’t know how to set up the equation. Pls help?

It’s trigonometry

Answer 1

`\displaystyle x \approx 47.44`

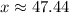
Explanation:

we are given a right angle triangle

we want to figure out x i.e hypotenuse

in order to do so we can consider trigonometry i.e sin

remember that,

`\displaystyle \sin( \theta) = (opp)/(hypo)`

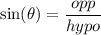
given that,theta=21° and opp=17 and hypo=x

Thus substitute:

`\displaystyle \sin( {21}^( \circ) ) = (17)/(x)`

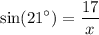
cross multiplication:

`\displaystyle x\sin( {21}^( \circ) ) = {17}`

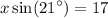
divide both sides by sin21°:

`\displaystyle x \frac{\sin( {21}^( \circ) ) }{ \sin( {21}^( \circ)) }= \frac{17}{ \sin( {21}^( \circ) ) }`

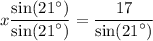
By using calculator we acquire:

`\displaystyle x \approx 47.44`