Question

G is a trigonometric function of the form g(x)=a sin (bx+c)+d.

The function intersects its midline at (-1 , 6) and has a minimum point at (-3.5 , 3)
Find a formula for g (x). Give an exact expression.

Answer 1

Formula for g(x) is
`g(x) = 3 sin((\pi )/(5)x + (\pi )/(5) ) + 6`

Explanation:

Given - g is a trigonometric function of the form g(x)=a sin (bx+c)+d. The function intersects its midline at (-1 , 6) and has a minimum point at (-3.5 , 3)

To find - Find a formula for g (x). Give an exact expression.

Proof -

Given that,

g(x)=a sin (bx+c)+d

We know that, Midline is present in between maximum and minimum

Here given that, minimum is present is 3 and midline is present at 6

So, Maximum occurs at 9.

Now,

We know that,

Standard form of sine function is - g(x) = Asin(B(x-C)) + D

Where

A = Amplitude

and Amplitude = (Maximum - minimum) / 2

= (9 - 3)/ 2

= 6/2 = 3

⇒A = 3

Now,

Period =
`(2\pi )/(B)`

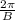
⇒B = (2π) / Period

= (2π) / 10

= π/5

⇒B = π/5

Now,

Phase Shift : C = -1 ( i.e. 1 to the left)

Vertical Shift : D = 6

So,

We get

g(x) = Asin(B(x-C)) + D

=
`3 sin((\pi )/(5)(x -(- 1))) + 6`

⇒
`g(x) = 3 sin((\pi )/(5)x + (\pi )/(5) ) + 6`

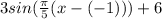
∴ we get

Formula for g(x) is
`g(x) = 3 sin((\pi )/(5)x + (\pi )/(5) ) + 6`