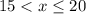Answer:
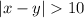 ---- Nita wins
---- Nita wins
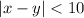 --- Eric wins
--- Eric wins
Explanation:
The complete instruction is to determine the range at which Erik or Nita wins.
To start with, let
 Erik's score
Erik's score
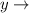 Nita's score
Nita's score
If the difference is greater than 10, the Nita wins.
This implies that:
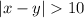 ---- Nita
---- Nita
If less than 10, then Eric wins
This implies that:
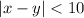 --- Eric wins
--- Eric wins
Now, assume that Nita chose 5.
For Nita to win, we have:
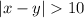
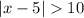
Remove the absolute symbol
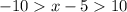
Split
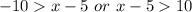
Solve for x
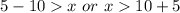
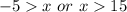
Rewrite as:
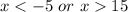
x cannot be negative.
So:

x cannot exceed 20.
So: