Question

Solve for the length of x

Answer 1

`\boxed {\boxed {\sf x\approx 63.7}}`

Explanation:

This is a right triangle. We know this because there is a small square in the corner representing a 90 degree/right angle. Therefore, we can use the right triangle trigonometry ratios.

• sinθ= opposite/hypotensue
• cosθ= adjacent/hypotenuse
• tanθ= opposite/adjacent

We are given angle A which measures 37 degrees.

Side BC which measures 48 is opposite angle A and the unknown side, x, is next to or adjacent to angle A.

We should use tangent.

`tan \theta= (opposite)/(adjacent)}`

`tan37= \frac {48}{x}`

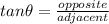
Since we are solving for x, we must isolate the variable. First, cross multiply. Multiply the first numerator and the second denominator, then the first denominator and second numerator.

`\frac {tan37}{1}=\frac {48}{x}`

`tan37*x=48*1`

`tan37*x= 48`

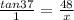
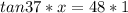
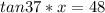
x is being multiplied by the tangent of 37. The inverse of multiplication is division, so we divide both sides by the tangent of 37.

`\frac {tan37 *x}{tan37}=(48)/(tan37)`

`x= (48)/(0.7535540501)}`

`x=63.69815144`

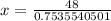
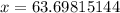
Even though it is not specified, let's round to the nearest tenths place. The 9 in the hundredth place tells us to round the 6 up to a 7.

`x\approx 63.7`

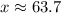
The unknown side is approximately 63.7 units long.