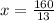Question

Which variable will you choose to eliminate? How? -3x -8y=-24 and
3x - 5y= 45

Answer 1

Lets choose y

• -8y=3x-24
• y=-3/8x+3

Plug in

• 3x+15/8x-15=45
• 39/8x= 60
• x=480/39

Answer 2

I'll choose 'x' variable first to eliminate because -

• -3 (coefficient of 'x' in Eqn.1) & 3 (coefficient of 'x' in Eqn.2) are additive inverses of each other , so they can be easily eliminated by simply adding those equations.
• It can be also solved by using elimination method but you'll need to multiply -1 with either Eqn.1 or Eqn.2 because in elimination method , a variable can be eliminated only when their coefficients are numerically equal (along with their sign).

Explanation:

Eqn.1 → -3x - 8y = -24

Eqn.2 → 3x - 5y = 45

If we'll add both the equations , then '3x' would be getting cancelled first.

⇒
`(-3x - 8y) + (3x - 5y) = (-24) + (45)`

⇒
`3x - 3x - 8y - 5y = 45 - 24`

⇒
`-13y = 21`

⇒
`y = (-21)/(13)`

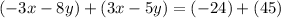
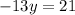
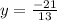
Putting the value of y in eqn.2 ,

⇒
`3x - 5((-21)/(13)) = 45`

⇒
`3x + (105)/(13) = 45`

⇒
`3x = 45 - (105)/(13)`

⇒
`3x = (585 - 105)/(13) = (480)/(13)`

⇒
`x = (480)/(13 * 3) = (480)/(39)`

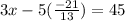
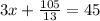
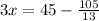
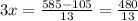
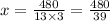
Reducing the fraction gives ,

⇒
`x = (160)/(13)`