Answer:
They are similar by the definition of similarity in terms of a dilation
Explanation:
The given vertices of triangle ΔABC are;
A(1, 5), B(3, 9), and C(5, 3)
The vertices of triangle ΔDEF are;
D(-3, 3), E(-2, 5), and F(-1, 2)
Therefore, we get;
The length of segment,
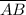 = √((9 - 5)² + (3 - 1)²) = 2·√5
= √((9 - 5)² + (3 - 1)²) = 2·√5
The length of segment,
 = √((9 - 3)² + (3 - 5)²) = 2·√10
= √((9 - 3)² + (3 - 5)²) = 2·√10
The length of segment,
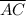 = √((5 - 3)² + (1 - 5)²) = 2·√5
= √((5 - 3)² + (1 - 5)²) = 2·√5
The length of segment,
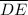 = √((5 - 3)² + (-2 - (-3))²) = √5
= √((5 - 3)² + (-2 - (-3))²) = √5
The length of segment,
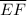 = √((2 - 5)² + (-1 - (-2))²) = √10
= √((2 - 5)² + (-1 - (-2))²) = √10
The length of segment,
 = √((2 - 3)² + (-1 - (-3))²) = √5
= √((2 - 3)² + (-1 - (-3))²) = √5
∴
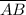 /
/
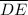 = 2·√5/(√5) = 2
= 2·√5/(√5) = 2
 /
/
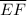 = 2·√10/(√10) = 2
= 2·√10/(√10) = 2
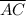 /
/
 = 2·√5/(√5) = 2
= 2·√5/(√5) = 2
The ratio of their corresponding sides are equal and therefore;
ΔABC and ΔDEF are similar by the definition of similarity in terms of dilation.