Answer:
The appropriate solution is "95%".
Explanation:
The given values are:
Lower bound,
= 173.8
Upper bound,
= 196.2
Mean of cholesterol,
= 138 milligrams
S = 17.6 mg
Now,
The margin of error (E) will be:
=
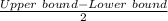
=
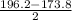
=
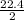
=
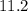
As we know,
⇒
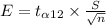
On putting the values, we get
⇒
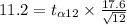
On applying cross-multiplication, we get
⇒
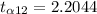
∴
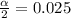
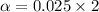
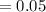
hence,
The confidence level will be:
⇒
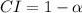
⇒

⇒
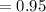
⇒
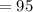 %
%