Question

A microscope has an objective lens with diameter 1.04 cm. You wish to resolve an object 9.09 micrometers in size. You are using visible light of wavelength 562 nm. Using the Rayleigh criterion, what is the distance that the objective lens must be from the object to resolve it

Answer 1

L = 0.1379 m = 13.79 cm

Step-by-step explanation:

The Rayleigh criterion establishes that two objects are separated when the maximum of diffraction for slits coincides with the minimum of the other point, therefore the expression for the diffraction

a sin θ = m λ

the first zero occurs when m = 1

let's use trigonometry to find the angle

tan θ = y / L

as in these experiments the angles are very small

tan θ = sin θ /cos θ = sin θ

sin θ = y / L

we substitute

a y /L = λ

In the case of circular aperture the system must be solved in polar coordinates, for which a numerical constant is introduced

a y / L = 1.22 λ

L = a y / 1.22 λ

We search the magnitudes to the SI system

a = 1.04 cm = 1.04 10⁻² m

y = 9.09 10⁻⁶ m

λ = 562 10⁻⁹ m

let's calculate

L =
`(1.04 \ 10^(-2) \ 9.09 \ 10^(-6) )/(1.22 \ 562 \ 10^(-9) )`

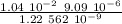
L = 1.379 10⁻¹ m

L = 0.1379 m = 13.79 cm