Question

A Carnot engine uses a steam boiler at 100°C as the high-temperature reservoir. The low-temperature reservoir is the outside environment at 35.0°C. Energy is exhausted to the low-temperature reservoir at a rate of 150 W. Hint (a) Determine the efficiency of the engine. (Give your answer as a percentage.) eC = % (b) Determine the useful power output of the heat engine (in W). output = W (c) How much steam (in kg) will it cause to condense in the high-temperature reservoir in 2.00 h? condensate = kg

Answer 1

(a) η = 0.1742 = 17.42 %

(b) W = 31.64 W

(c) m = 0.58 kg

Step-by-step explanation:

(a)

The efficiency of a Carnot's engine is given as follows:

`\eta = 1-(T_2)/(T_1)`

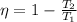
where,

η = efficiency = ?

T₁ = source temperature = 100°C + 273 = 373 K

T₂ = sink temperature = 35°C + 273 = 308 K

Therefore,

`\eta = 1 - (308\ k)/(373\ k) \\`

η = 0.1742 = 17.42 %

(b)

Another formula for the efficiency of Carnot's Engine is:

`\eta = 1 - (Q_2)/(Q_1)`

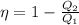
where,

Q₁ = Input heat rate

Q₂ = Heat rejected = 150 W

Therefore,

`0.1742 = 1 - (150\ W)/(Q_1)\\\\ (150\ W)/(Q_1) = 1-0.1742\\\\Q_1 = (150\ W)/(0.8258)`

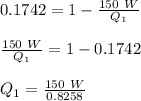
Q₁ = 181.64 W

Now, for the useful power output:

`W = Q_1-Q_2\\W = 181.64\ W - 150\ W\\W = 31.64\ W`

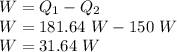
where,

W = Useful Output

W = 31.64 W

(c)

The heat required to condense steam i given as:

`Q = mH\\Q_1t=mH\\m = (Q_1t)/(H)`

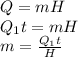
where,

m = mass of steam condensed = ?

t = time = 2 h = 7200 s

H = Latent heat of condensation of steam = 2260 KJ/kg = 2260000 J/kg

Therefore,

`m = ((181.64\ W)(7200\ s))/((2260000\ J/kg))`

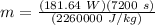
m = 0.58 kg