Question

Mhanifa please help! Find the missing side. Round to the nearest tenth

Answer 1

12) x = 49.5

13) x = 8.5

14) x = 44.8

15) x = 4.6

Explanation:

We can solve for the missing side lengths using trigonometry

Remember these are the trigonometric ratios

Sin = Opposite over Hypotenuse

Cos = Adjacent over Hypotenuse

Tan = Opposite over Adjacent

For #12

We can use trig ratio tangent as we are given an angle with a measure of 68° and its adjacent side length and we need to find the opposite side length. When dealing with opposite and adjacent we can use tan.

That being said we want to create an equation to solve for x

`tan(68)=(x)/(20)`

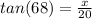
Now we solve

* multiply each side by 20 *

`20tan(68) = 49.5\\(x)/(20) 20=x\\`

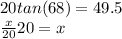
we're left with x = 49.5

It seems that all of the problems are dealing with an angle, its opposite side and its adjacent side. So we will use the same trig ratio "tan" and process to solve for x.

For 13)

`tan(62)=(16)/(x) \\`

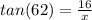
*multiply each side by x*

`xtan(62)=16`

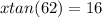
*divide each side by tan(62)

`(xtan(62))/(tan(62)) =x\\(16)/(tan(62)) =8.5`

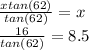
we're left with x = 6.5

For 14)

`tan(15)=(12)/(x)`

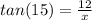
multiply each side by x

`xtan(15)=12`

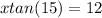
divide each side by tan15

`(xtan(15))/(tan(15)) =x\\(12)/(tan(15)) =44.8`

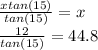
we're left with x = 44.8

For 15)

`tan(74)=(16)/(x)`

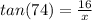
multiply each side by x

`xtan(74)=16`

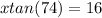
divide each side by tan(74)

`(xtan(74))/(tan74) =x\\(16)/(tan(74)) =4.6`

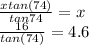
we're left with x = 4.6