Answer:
Indeed, the given triangle is a right triangle.
Explanation:
A triangle is formed by the following three points:
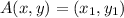 ,
,
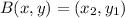 and
and
 . Then, we construct the following vectors:
. Then, we construct the following vectors:
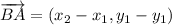
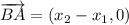 (1)
(1)
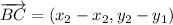
 (2)
(2)
If triangle ABC is a right triangle, then
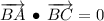 . By (1) and (2) we have this expression:
. By (1) and (2) we have this expression:
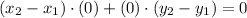
Therefore, the given triangle is a right triangle.