Question

A fly is standing on a boulder, which is rolling down a hill. The forward torque the fly exerts on the boulder when it has rolled x xx meters, in newton meters, is given by τ ( x ) = 2 1000 sin ⁡ ( 2 π ( x + 0.2 ) 4 ) τ(x)= 1000 2 ​ sin( 4 2π(x+0.2) ​ )tau, left parenthesis, x, right parenthesis, equals, start fraction, 2, divided by, 1000, end fraction, sine, left parenthesis, start fraction, 2, pi, left parenthesis, x, plus, 0, point, 2, right parenthesis, divided by, 4, end fraction, right parenthesis. What is the midline of this function? Give an exact answer. y =

Answer 1

Question:

A fly is standing on a boulder which is rolling down a hill. The forward torque the fly exerts on the boulder when it has rolled 'x' meters, in Newton meters is given by

`\tau(x) = (2)/(1,000) \cdot sin \left((2 \cdot \pi \cdot (x + 0.2))/(4) \right )`

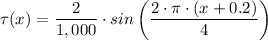
Answer:

y = 0

Explanation:

The general form of the sine function is presented as follows;

y = A·sin[B·(x - C)] + D

Where;

A = The amplitude

C = The horizontal shift

D = The vertical shift above the generic midline of y = 0 = Constant

By comparison with the general equation for torque, we have that the constant D = 0, therefore, the vertical shift = 0, and the midline of the the given function = The midline of the generic sine function which is y = 0.