Answer: 0.84134
Explanation:
We need to find the z-score for the given information first since this will help us find the probability. The formula for this is
Z score =

We have
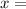 66 inches (the raw score)
66 inches (the raw score)
 70 inches (the population mean)
70 inches (the population mean)
 = 4 inches (the standard deviation)
= 4 inches (the standard deviation)
This gives
Z score =
 =
=

If you use a calculator, or a Z-score table then P(x > Z) is just P(Z > -1) which gives a probability of 0.84134.