Question

Consider a city whose streets are laid out as a grid. Streets run north-south or east-west. A visitor is dropped off by a cab at a certain intersection and would like to visit a museum that is 6 blocks to the east and 3 blocks to the north of his current location. The visitor always takes a direct path and never travels west or south in the course of his walk. How many distinct paths are there for the visitor to walk to the museum

Answer 1

84 possible paths

Explanation:

Given

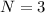`N =3` --- 3 blocks north

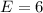`E = 6` --- 6 blocks east

Required

Number of distinct path

To solve this question, we make use of the following formula

`^(m+n)C_n \ =\ ^(m+n)C_m`

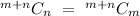
The above formula implies that;

On a single path, there is a total of m + n steps to get to a particular position, where each path is either in m direction or n direction.

In this case:

`m = 3`

`n = 6`

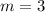
So, we have:

`^(m + n)C_n = ^(3+6)C_6`

`^(m + n)C_n = ^9C_6`

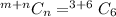
Apply combination formula

`^(m + n)C_n = (9!)/((9-6)!6!)`

`^(m + n)C_n = (9!)/(3!*6!)`

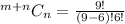
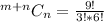
Expand the numerator

`^(m + n)C_n = (9*8*7*6!)/(3!*6!)`

`^(m + n)C_n = (9*8*7)/(3!)`

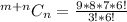
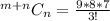
Expand the denominator

`^(m + n)C_n = (9*8*7)/(3*2*1)`

`^(m + n)C_n = (504)/(6)`

`^(m + n)C_n = 84`

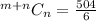
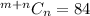
Hence, there are 84 possible paths

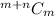`^(m + n)C_m` will also give the same result