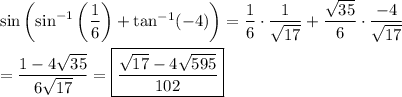Question

Find the exact value of the​ following, without using a calculator.

Answer 1

9514 1404 393

Answer:

(√17 -4√595)/102

Explanation:

To use the sine of the angle sum formula, we need to know the sine and cosine of each of the angles.

sin(sin^-1(1/6)) = 1/6 . . . . a first-quadrant angle

cos(sin^-1(1/6)) = √(1 -(1/6)²) = √(35/36) = (√35)/6

sin(tan^-1(-4)) = -4/√(1+(-4)²) = -4/√17 . . . . a 4th-quadrant angle

cos(tan^-1(-4)) = √(1 -(-4/√17)²) = 1/√17

The sum of angles formula is ...

sin(α+β) = sin(α)cos(β) +cos(α)sin(β)

So, our sine is ...

`\sin\left(\sin^(-1)\left((1)/(6)\right)+\tan^(-1)(-4)\right)=(1)/(6)\cdot(1)/(√(17))+(√(35))/(6)\cdot(-4)/(√(17))\\\\=(1-4√(35))/(6√(17))=\boxed{(√(17)-4√(595))/(102)}`