Question

What is the area of the isosceles triangle shown?

Answer 1

672

Explanation:

Area of a triangle =
`(bh)/(2)`

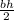
where b = base length and h = height

In the triangle shown, we are only given the base length

This means that we must find the height in order to find the area.

We can do this by using the Pythagorean theorem

`a^2+b^2=c^2`

where a and b = legs and c = hypotenuse

Two right triangles are formed within the isosceles triangle.

Each has a hypotenuse of 50 m, a base length of 28/2=14m ( because they are sharing the base length ) and they are both sharing the height.

So we are given the hypotenuse and a leg and we need to find the other leg

So we plug in what we are given and solve for the missing side length

`50^2=a^2+14^2\\50^2=2500\\14^2=196\\2500=a^2+196`

step 1 subtract 196 from each side

2500 - 196 = 2304

196 - 196 cancels out

we now have 2304 = a²

step 2 take the square root of each side

`√(a^2) =a\\√(2304) =48`

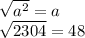
we're left with a = 48

This means that the height of the isosceles triangle is 48m

Now we can find the area.

Using the formula stated previous....

`A=(28*48)/(2) \\28*48=1344\\(1344)/(2) =672`

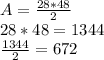
Hence, the area is 672m²

Answer 2

672 meters squared

Explanation:

Area of Triangle: b*h*1/2

The isosceles triangle's height, splits the base in half.