Answer:
(c) The triangles are similar, so the sides are proportional: DE = BC. Therefore, the slope of AD is the same as the slope of AB
Explanation:
Given
See attachment for proper format of question
Required
Why is the slope between A and D the same
From the question, we understand that:
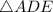 and
and
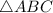 are similar
are similar
This implies that similar sides are proportional.
i.e.



Slope (m) is calculated as:
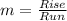
So, the slope of
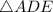 is:
is:
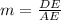
Slope of
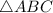 is:
is:
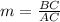
Since the triangles are similar, then:

i.e.

Hence, (c) is true