Question

A study was conducted and two types of engines, A and B, were compared. Fifty experiments were performed using engine A and 75 using B. The average gas mileage for A was 36 mpg, and 42 mpg for B. Assume population standard deviations for A and B are respectively 6 and 8. A. Find the point estimate. (2 pts) B. Find the margin of error. (3 pts) C. Construct the 95% confidence interval for the difference of population mean gas mileages for engines A and B and interpret the results(5 pts)

Answer 1

a) -6 mpg.

b) 2.77 mpg

c) The 95% confidence interval for the difference of population mean gas mileages for engines A and B and interpret the results, in mpg, is (-8.77, -3.23).

Explanation:

To solve this question, we need to understand the central limit theorem, and subtraction of normal variables.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

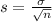For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
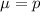`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

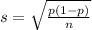
Subtraction between normal variables:

When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.

Gas mileage A: Mean 36, standard deviation 6, sample of 50:

So

`\mu_A = 36, s_A = (6)/(√(50)) = 0.8485`

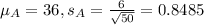
Gas mileage B: Mean 42, standard deviation 8, sample of 50:

So

`\mu_B = 42, s_B = (8)/(√(50)) = 1.1314`

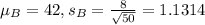
Distribution of the difference:

Mean:

`\mu = \mu_A - \mu_B = 36 - 42 = -6`

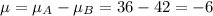
Standard error:

`s = √(s_A^2+s_B^2) = √(0.8485^2+1.1314^2) = 1.4142`

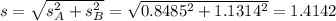
A. Find the point estimate.

This is the difference of means, that is, -6 mpg.

B. Find the margin of error

We have that to find our
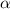`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1 - 0.95)/(2) = 0.025`

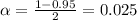
Now, we have to find z in the Ztable as such z has a pvalue of
`1 - \alpha`.

That is z with a pvalue of
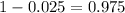`1 - 0.025 = 0.975`, so Z = 1.96.

Now, find the margin of error M as such

`M = zs = 1.96*1.4142 = 2.77`

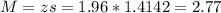
The margin of error is of 2.77 mpg

C. Construct the 95% confidence interval for the difference of population mean gas mileages for engines A and B and interpret the results(5 pts)

The lower end of the interval is the sample mean subtracted by M. So it is -6 - 2.77 = -8.77 mpg

The upper end of the interval is the sample mean added to M. So it is -6 + 2.77 = -3.23 mpg

The 95% confidence interval for the difference of population mean gas mileages for engines A and B and interpret the results, in mpg, is (-8.77, -3.23).