Answer:

Explanation:
We want to solve the equation:
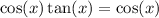
On the interval [0, 2π).
First, we can subtract cos(x) from both sides:
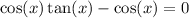
Factor:
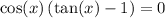
Zero Product Property:

Solve for each case:

Using the unit circle:
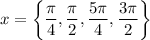
However, since tangent isn't defined for π/2 and 3π/2, we remove them from our solutions. Hence:
