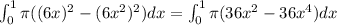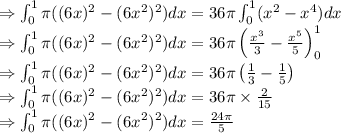Answer:
Hence, the Area is

Explanation:
Concept :
Area of the region bounded by two curve :
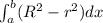
volume of the solid generated by revolving the region about the x-axis is :
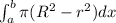 where
where
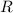 is long radius of bounded region from x-axis and
is long radius of bounded region from x-axis and
 is short radius of bounded region from x-axis.
is short radius of bounded region from x-axis.
Given :
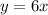 and
and
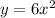
To find :
Area of the region bounded by
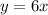 and
and
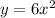 and volume of the solid generated by revolving the region about the x-axis.
and volume of the solid generated by revolving the region about the x-axis.
Explanation :
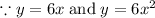
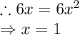
Area of the region bounded by
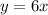 and
and
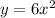 is :
is :
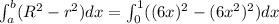
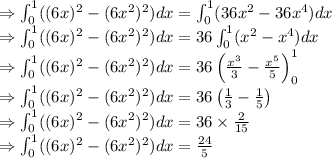
Volume of the solid generated by revolving the region about the x-axis.