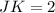Answer:
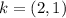
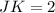
Explanation:
Given
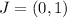 ----
----

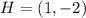 ---
---

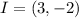 ---
---
See attachment for grid
Solving (a): The coordinates of K
The parallelogram has the following diagonals: IJ and HK
Diagonals bisect one another. So:
Midpoint of IJ = Midpoint of HK
This gives:

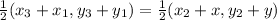
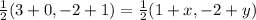

Multiply through by 2
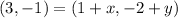
By comparison:
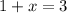
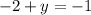
Solve for x and y
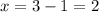

So, the coordinates of k is:
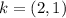
The length of JK is calculated using distance (d) formula
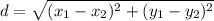
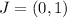 ----
----

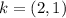 ----
----

So:
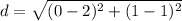
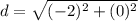
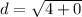
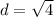
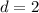
Hence: