Question

Solve the equation for exact solutions over the interval​ [0, 2π​).

Answer 1

`\displaystyle x=\left\{0, (2\pi)/(3), (4\pi)/(3)\right\}`

Explanation:

We want to solve the equation:

`-2\cos^2(x)=-\cos(x)-1`

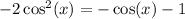
Over the interval [0, 2π).

First, notice that this is in quadratic form. So, to make things simpler, we can let u = cos(x). Substitute:

`-2u^2=-u-1`

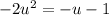
Rearrange:

`2u^2-u-1=0`

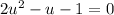
Factor:

`(2u+1)(u-1)=0`

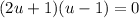
Zero Product Property:

`2u+1=0\text{ or } u-1=0`

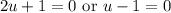
Solve for each case:

`\displaystyle u=-(1)/(2)\text{ or } u=1`

Back-substitute:

`\displaystyle \cos(x)=-(1)/(2)\text{ or } \cos(x)=1`

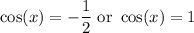
Using the unit circle:

`\displaystyle x=\left\{0, (2\pi)/(3), (4\pi)/(3)\right\}`