Answer:
Vector (ordered pair - rectangular form)
![\vec F = (27.189,12.679)\,[lbf]](https://img.qammunity.org/2022/formulas/mathematics/high-school/p17k8klq3xjzxfsa20a5rvxm2tch0dbxko.png)
Vector (ordered pair - polar form)
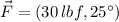
Sum of vectorial components (linear combination)
![\vec F = 27.189\cdot \hat{i} + 12.679\cdot \hat{j}\,[N]](https://img.qammunity.org/2022/formulas/mathematics/high-school/nnktr9xsq34hg9lfjpb1xxaj76bkd9mwql.png)
Explanation:
From statement we know that force exerted on the wagon has a magnitude of 30 pounds-force and an angle of 25° above the horizontal, which corresponds to the +x semiaxis, whereas the vertical is represented by the +y semiaxis.
The force (
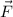 ), in pounds-force, can be modelled in two forms:
), in pounds-force, can be modelled in two forms:
Vector (ordered pair - rectangular form)
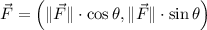 (1)
(1)
Vector (ordered pair - polar form)
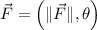
Sum of vectorial components (linear combination)
 (2)
(2)
Where:
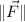 - Norm of the vector force, in newtons.
- Norm of the vector force, in newtons.
 - Direction of the vector force with regard to the horizontal, in sexagesimal degrees.
- Direction of the vector force with regard to the horizontal, in sexagesimal degrees.
 ,
,
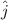 - Orthogonal axes, no unit.
- Orthogonal axes, no unit.
If we know that
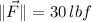 and
and
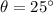 , then the force exerted on the wagon is:
, then the force exerted on the wagon is:
Vector (ordered pair - rectangular form)
![\vec F= \left(30\cdot \cos 25^(\circ), 30\cdot \sin 25^(\circ)\right)\,[lbf]](https://img.qammunity.org/2022/formulas/mathematics/high-school/oz59n5vqykks97jwsry17ht7ll3iqqol1v.png)
![\vec F = (27.189,12.679)\,[lbf]](https://img.qammunity.org/2022/formulas/mathematics/high-school/p17k8klq3xjzxfsa20a5rvxm2tch0dbxko.png)
Vector (ordered pair - polar form)
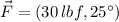
Sum of vectorial components (linear combination)
![\vec F = (30\cdot \cos 25^(\circ))\cdot \hat{i} + (30\cdot \sin 25^(\circ))\cdot \hat{j}\,[N]](https://img.qammunity.org/2022/formulas/mathematics/high-school/sgomp5un4ij8y83eoy062dwnv01m8askji.png)
![\vec F = 27.189\cdot \hat{i} + 12.679\cdot \hat{j}\,[N]](https://img.qammunity.org/2022/formulas/mathematics/high-school/nnktr9xsq34hg9lfjpb1xxaj76bkd9mwql.png)