Question

An exponential function is given by the equation y=3x. Using the points xx and x+1x+1, show that the y-values increase by a factor of 3 between any two points separated by x2−x1=1.(4 points)

Answer 1

Here we have the function:

y = f(x) = 3^x

Using the values:

x and (x + 1)

We need to find that the y-value increases by a factor of 3.

So we need to prove that:

f(x + 1) = 3*f(x).

Or we can see the quotient:

f(x + 1)/f(x) = 3

Here we can find the values:

f(x + 1) = y = 3^(x + 1)

f(x) = y' = 3^x

If we take the quotient, we get:

`(f(x + 1))/(f(x)) = (3^(x + 1))/(3^x)`

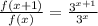
Here we can use the properties:

`a^n*a^m = a^(n + m)`

`(a^n)/(a^m) = a^(n - m)`

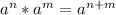
Using these in the quotient equation we get:

`(f(x + 1))/(f(x)) = (3^(x + 1))/(3^x) = (3^x*3^1)/(3^x) = (3^x)/(3^x)*3 = 1*3 = 3`

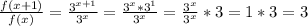
Then:

`(f(x + 1))/(f(x)) = 3`

`f(x + 1) = 3*f(x)`

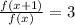
So we found that the y-value increases by a factor of 3 between any two points x₂ and x₁ such that: x₂ - x₁ = 1.