Question

A model rocket is launched with an initial upward velocity of 188 ft/s. The rocket's height h (in feet) after t seconds is given by the following.

h=188t-16t^2

Find all values of for which the rocket's height is 92 feet.
Round your answer(s) to the nearest hundredth.
(If there is more than one answer, use the "or" button.)

Answer 1

0.51 and 11.24 seconds.

Explanation:

The height h of a rocket with an initial upward velocity of 188 feet per second after t seconds is modeled by the function:

`h(t)=188t-16t^2`

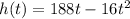
And we want to find all values of t for which the rocket's height is 92.

So, we can set h(t) = 92 and solve for t:

`92=188t-16t^2`

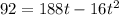
We can divide everything by four:

`23=47t-4t^2`

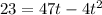
Rearrange the equation:

`4t^2-47t+23=0`

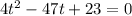
We can use the quadratic formula:

`\displaystyle x=(-b\pm√(b^2-4ac))/(2a)`

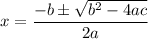
In this case, a = 4, b = -47, and c = 23. Substitute:

`\displaystyle x=(-(-47)\pm√((-47)^2-4(4)(23)))/(2(4))`

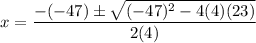
Evaluate:

`\displaystyle x=(47\pm√(1841))/(8)`

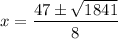
Hence, our two solutions are:

`\displaystyle x=(47+√(1841))/(8)\approx 11.24\text{ or } x=(47-√(1841))/(8)\approx0.51`

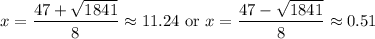
So, the rocket reaches a height of 92 feet after 0.51 seconds and again after 11.24 seconds.