Answer:
Outside, as the distance between the point and the center of the circle is more than the radius.
Explanation:
Equation of a circle:
The equation of a circle has the following format:
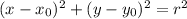
In which
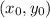 is the center and r is the radius.
is the center and r is the radius.
Testing if a point is inside the circle:
Point (x,y), we replace in the equation. If it is less than the radius squared(in this case, 62), it is in.
In this question:
Point (-3,-5). So
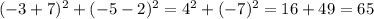
The square distance of the point to the center is of 65, which is more than the square of the radius, meaning that the point is outside the circle.