Question

A physical therapist wants to determine the difference in the proportion of men and women who participate in regular sustained physical activity. What sample size should be obtained if she wishes the estimate to be within three percentage points with 99​% ​confidence, assuming that ​(a) she uses the estimates of 22.6​% male and 18.1​% female from a previous​ year

Answer 1

A sample size of 1380 should be obtained.

Explanation:

Minimum sample size:

The minimum sample size is of:

`n = ((z)/(E))^2(p_1(1-p_1) + p_2(1-p_2))`

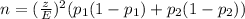
In which z is the critical value, related to the confidence level, E is the desired margin of error,
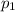`p_1` and
`p_2` are the proportions.

99% confidence level

So
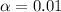`\alpha = 0.01`, z is the value of Z that has a pvalue of
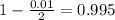`1 - (0.01)/(2) = 0.995`, so
`Z = 2.575`.

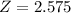Estimates of 22.6​% male and 18.1​% female from a previous​ year

This means that
`p_1 = 0.226, p_2 = 0.181`.

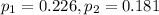Within 3 percentage points, minimum sample size:

This is n for which
`E = 0.03`. So

`n = ((z)/(E))^2(p_1(1-p_1) + p_2(1-p_2))`

`n = ((1.96)/(0.03))^2(0.226*0.774 + 0.181*0.819)`

`n = 1379.4`

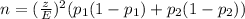
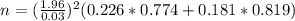
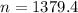
Rounding up:

A sample size of 1380 should be obtained.