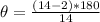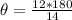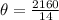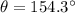Answer:
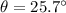 --- Measure of each exterior angle
--- Measure of each exterior angle
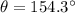 --- Measure of each interior angle
--- Measure of each interior angle
Explanation:
Given [Missing from the question]
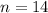 --- number of sides
--- number of sides
Required
- The measure of an exterior angle
- The measure of an interior angle
For an n-sided polygon, the measure of each exterior angle is:

Substitute 14 for n
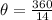
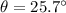
For an n-sided polygon, the measure of each interior angle is:
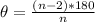
Substitute 14 for n