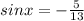Question

A circle centered at the origin has a radius of 13. The terminal side of an angle x, intercepts the circle in quadrant IV at point C. The x coordinate of point C is 12. What is the value of sin x

Answer 1

`sin x=-(5)/(13)`

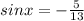
Explanation:

From the question we are told that:

Radius
`r=13`

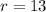
Co-ordinate of x axis at C
`x'=12`

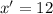
Let

x' represent the x axis

y' represent the y axis

Since the intercept across the radius has values on the x' and y' axis

Therefore

Generally the Trigonometric equation for cos x is mathematically given by

`cos x=(x'_c)/(r)`

`cos x=(12)/(13)`

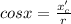
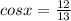
Generally the Trigonometric equation for sin x is mathematically given by

`sin x=√(1-cos^2x)`

`sin x=\sqrt{1-((12)/(13))^2}`

`sin x=(5)/(13)`

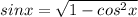
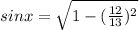
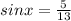
Since x is in the IV quadrant sin x is negative

`sin x=-(5)/(13)`