Answer:
The distance from point A to B that Haley needs for the pole to be perpendicular is:
Explanation:
To solve this exercise, imagine that it is a triangle, where the height is the pole, which is 10 feet, and the base of the triangle is the distance between the base of the pole and the point located by Jalen and called C, which it would have a measurement of 6 feet, finally, the measurement between A (the point located six feet) and B (the highest part of the pole) would correspond to the hypotenuse of a triangle,
Therefore, having these two measures, you could use the Pythagorean theorem to find the hypotenuse of a triangle with those measures and solve it, remember that the Pythagorean theorem is:
- Hypotenuse^2 = opposite leg^2 + adjacent leg^2
We replace the values given in the exercise:
- Hypotenuse^2 = (10 ft)^2 + (6 ft)^2
- Hypotenuse^2 = 100 ft^2 + 36 ft^2
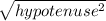 =
=
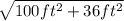
- Hypotenuse =
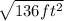
- Hypotenuse = 11.66 ft approximately.
In this form, Jalen can be sure the pole is perpendicular to the ground when the distance from point A to B is 11.66 ft approximately.