Question

Please help! find the common ratio of the geometric sequence. -1/4, 1/16, -1/64, 1/256,... A. 1/64 B. -1/4 C. -1/16 D. 1/16 E. 1/4​

Answer 1

Answer: B) -1/4

=====================================================

Step-by-step explanation:

Pick any term of the sequence that isn't the first term. Divide whatever you picked by the previous term. That will compute the common ratio. This applies to geometric sequences only.

So let's say we pick on term 3 and divide it over term 2. That will get us...

`r = \left(\text{3rd term}\right) / \left(\text{2nd term}\right)\\\\r = -(1)/(64) / (1)/(16)\\\\r = -(1)/(64) * (16)/(1)\\\\r = (-1*16)/(64*1)\\\\r = -(16)/(64)\\\\r = -(16)/(16*4)\\\\r = -(1)/(4)\\\\`

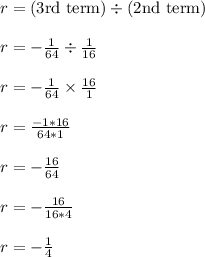
Where r is the common ratio.

As another example, let's say we picked on term 4 and divided it over the third term

`r = \left(\text{4th term}\right) / \left(\text{3rd term}\right)\\\\r = (1)/(256) / -(1)/(64)\\\\r = (1)/(256) * -(64)/(1)\\\\r = (1*(-64))/(256*1)\\\\r = -(64)/(256)\\\\r = -(64)/(64*4)\\\\r = -(1)/(4)\\\\`

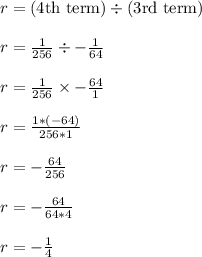
We get the same result. I'll let you try dividing the second term over the first term. You should get r = -1/4 after simplifying.

-------------

Because the common ratio is r = -1/4, this means that we multiply each term by the common ratio to generate the next term.

For instance,

term 3 = (term 2)*(common ratio)

term 3 = (1/16)*(-1/4)

term 3 = -1/64

which matches with the given sequence

Answer 2

B -1/4

Step-by-step explanation:

To find the common ratio, divide any term by the previous term.

1/16 ÷ -1/4 = 1/16 * -4 = -4/16 = -1/4