Question

Does anyone know what the monthly payment is?:/

Answer 1

Answer: 700.22 dollars

====================================================

Step-by-step explanation:

The formula given is

`M = (P*\left((r)/(12)\right)*\left(1+(r)/(12)\right)^(12*t))/(\left(1+(r)/(12)\right)^(12*t)-1)\\\\`

which to be honest is a big ugly mess of variables. The fractions also make things even more messy. Through trial and error, you can find various ways to help clean up the formula.

Notice how the "r/12" seems to show up a lot. Let's replace that fraction with the variable A.

So we'll make A = r/12

Because of that, the expression
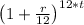`\left(1+(r)/(12)\right)^(12*t)` turns into
`\left(1+A\right)^(12*t)`

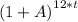
After replacing all the "r/12" terms with "A", we have the formula

`M = (P*\left((r)/(12)\right)*\left(1+(r)/(12)\right)^(12*t))/(\left(1+(r)/(12)\right)^(12*t)-1)\\\\`

turn into

`M = (P*A*\left(1+A\right)^(12*t))/(\left(1+A\right)^(12*t)-1)\\\\`

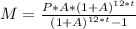
which is a bit simpler in my opinion.

------------------

We could also let

B = (1+A)^(12t)

which would then allow us to go from this

`M = (P*A*\left(1+A\right)^(12*t))/(\left(1+A\right)^(12*t)-1)\\\\`

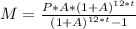
to this

`M = (P*A*B)/(B-1)\\\\`

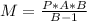
and that's even more simple

---------------------

We're given the following values

• P = 75,000 = amount loaned
• r = 0.023 = annual interest rate in decimal form
• t = 10 = number of years

Based on those values, we can say

• A = r/12 = 0.023/12 = 0.00191667 approximately
• B = (1+A)^(12*t) = (1+0.00191667)^(12*10) = 1.25832348 approximately

From here, we plug the values of P, A, and B into the simplified version of the formula below.

`M = (P*A*B)/(B-1)\\\\M \approx (75000*0.00191667*1.25832348)/(1.25832348-1)\\\\M \approx (180.88431483087)/(0.25832348)\\\\M \approx 700.22405563\\\\M \approx 700.22\\\\`

The monthly payment is roughly $700.22