Question

A muon is a type of subatomic particle. If a muon is at rest in the laboratory, it will decay into an electron after about 2 microseconds. Suppose an observer watches a muon travel through the atmosphere at 90% of the speed of light. How does the lifetime of the moving muon compare to the laboratory muon for an observer at rest with respect to the lab

Answer 1

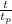`(t)/(t_p)` = 2.29

Step-by-step explanation:

For this exercise as the muon goes at speeds close to the speed of light we must use relativists

t =
`\frac{t_p}{\sqrt{1- ((v)/(c))^2 } }`

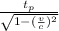
The proper time is the decay time in the reference frame where the muon is fixed ( laboratory), t_p = 2 10⁻⁶ s and the relation

v / c = 0.90

let's calculate

t =
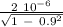`(2 \ 10^(-6) )/(√(1 \ - \ 0.9^2 ) )`2 10-6 / Ra (1 - 0.9²)

t = 4.59 10⁻⁶ s

the ralation is

`(t)/(t_p) = (4.59 \ 10^(-6))/( 2 \ 10^(-6))\\`

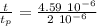
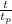`(t)/(t_p)` = 2.29