Answer:
![f(x) = 2[(3^x)/(9)] + 2](https://img.qammunity.org/2022/formulas/mathematics/high-school/d6heizaocixt0q5dus3oi40obrocaf1wes.png)

Explanation:
Given
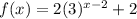

Required
Remove the h component
In a function, the h component is highlighted as:
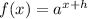
So, we have:
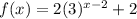
Split the exponents using the following law of indices:
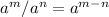
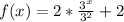
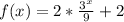
![f(x) = 2[(3^x)/(9)] + 2](https://img.qammunity.org/2022/formulas/mathematics/high-school/d6heizaocixt0q5dus3oi40obrocaf1wes.png)
The h component has been removed

Split the exponent using the following law of indices
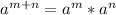
So, we have:

Express 4^2 as 16

Divide 16 by 2
