Answer:
22 sides
Explanation:
The expression to find an interior angle of a polygon is:
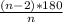
The expression to find an exterior angle of a polygon is:
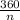
Please note that "n" represents the number of sides the polygon has.
We can use these two expressions to set up an equation.
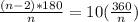
Multiply both sides by "n":
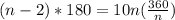
Now, distribute:

Divide both sides by 10:
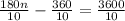

Add 36 to both sides:

Divide both sides by 18:

The polygon has 22 sides