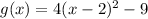Answer:
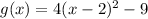
Explanation:
Given
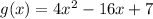
Required
Complete the square
Rewrite so that
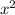 has 1 coefficient
has 1 coefficient
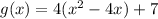
Take half of the coefficient of x
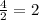
Square the result
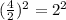
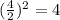
Add and subtract the result in the bracket
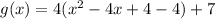
Expand the bracket to remove -4
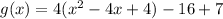

Expand the bracket
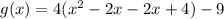
Factorize
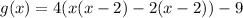
Factor out x - 2
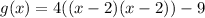
Express as square