Question

Rewrite the function by completing the square.

g(x)=4x^2-16x+7


g(x)=___(x+___)^2+__

Answer 1

`g(x) = 4(x - 2)^2 -9`

Explanation:

Given

`g(x) = 4x^2 - 16x + 7`

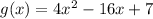
Required

Complete the square

Rewrite so that
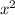`x^2` has 1 coefficient

`g(x) = 4(x^2 - 4x) + 7`

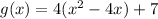
Take half of the coefficient of x

`(4)/(2) = 2`

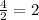
Square the result

`((4)/(2))^2 = 2^2`

`((4)/(2))^2 = 4`

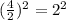
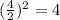
Add and subtract the result in the bracket

`g(x) = 4(x^2 - 4x + 4 - 4) + 7`

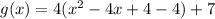
Expand the bracket to remove -4

`g(x) = 4(x^2 - 4x + 4) - 16 + 7`

`g(x) = 4(x^2 - 4x + 4) -9`

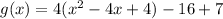
Expand the bracket

`g(x) = 4(x^2 - 2x -2x+ 4) -9`

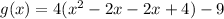
Factorize

`g(x) = 4(x(x - 2) -2(x-2)) -9`

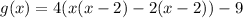
Factor out x - 2

`g(x) = 4((x - 2)(x-2)) -9`

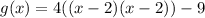
Express as square

`g(x) = 4(x - 2)^2 -9`