Question

a website would like to test the hypotheis that the average length of an online video watched by a user is more than 8 minutes. A random sample of 37 people watched onlinevideos that averaged 8.7 minutes in length. It is believed that the population standard deviation for the length of online videos is 2.5 minutes. The website owners would like to set =.02 what is the conclusion for this hyptohesis test

Answer 1

The p-value of the test is 0.0446 > 0.02, which means that we do not reject the null hypothesis that the average length of an online video watched by a user is of 8 minutes.

Explanation:

A website would like to test the hypothesis that the average length of an online video watched by a user is more than 8 minutes.

At the null hypothesis, we test if the mean is of 8 minutes, that is:

`H_0: \mu = 8`

At the alternate hypothesis, we test if the mean is of more than 8 minutes, that is:

`H_a: \mu > 8`

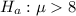
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

8 is tested at the null hypothesis:

This means that
`\mu = 8`

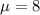
A random sample of 37 people watched online videos that averaged 8.7 minutes in length. It is believed that the population standard deviation for the length of online videos is 2.5 minutes.

This means that
`n = 37, X = 8.7, \sigma = 2.5`

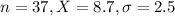
Test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (8.7 - 8)/((2.5)/(√(37)))`

`z = 1.70`

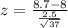
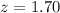
P-value of the test and decision:

The p-value of the test is the probability of finding a sample mean above 8.7, which is 1 subtracted by the p-value of z = 1.7.

Looking at the z-table, z = 1.7 has a p-value of 0.9554

1 - 0.9554 = 0.0446

The p-value of the test is 0.0446 > 0.02, which means that we do not reject the null hypothesis that the average length of an online video watched by a user is of 8 minutes.