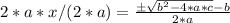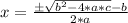Question

Please help !!!!!!

Clare is deriving the quadratic formula by solving ax^2+bx+c=0 by completing the square.
She arrived at this equation:
(2ax+b)^2=b^2-4ac
Briefly describe what she needs to do to finish solving for I and then show the steps.

Answer 1

Clare starts with:

a*x^2 + b*x + c = 0

And she gets to:

(2*a*x + b)^2 = b^2 - 4*a*c

Now we want to show the final steps to solve the equation (isolating x)

First, we apply the square root to both sides:

`√((2*a*x + b)^2) = √((b^2 - 4*a*c))`

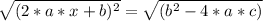
Because the square root has two solutions, (one negative and one positive), we will write:

`2*a*x + b = \pm √(b^2 - 4*a*c)`

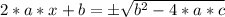
Now we subtract b in both sides:

`(2*a*x + b) - b = \pm √(b^2 -4*a*c) - b`

`2*a*x = \pm √(b^2 -4*a*c) - b`

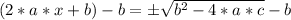
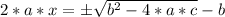
Now let's divide by 2*a in both sides:

`2*a*x/(2*a) = (\pm √(b^2 -4*a*c) - b)/(2*a)`

`x = (\pm √(b^2 -4*a*c) - b)/(2*a)`