Question

Triangle JKL has vertices J(0, 2), K(–1, 2), and L(0, –3). What are the coordinates of the image of point J after a dilation with a scale factor of 3?

Answer 1

Given:

The vertices of a triangle JKL are J(0, 2), K(–1, 2), and L(0, –3).

To find:

The coordinates of the image of point J after a dilation with a scale factor of 3.

Solution:

If a figure is dilated by a scale factor of k, then

`(x,y)\to (kx,ky)`

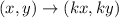
The given triangle JKL dilated by a scale factor of 3. So,

`(x,y)\to (3x,3y)`

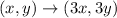
The coordinates of point J are J(0,2). By using the above rule, we get

`J(0,2)\to J'(3(0),3(2))`

`J(0,2)\to J'(0,6)`

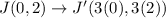
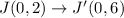
Therefore, the coordinates of the image of point J after a dilation with a scale factor of 3 are J'(0,6).