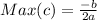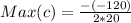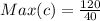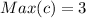Question

The power generated by an electrical circuit (in watts) as a function of its current ccc (in amperes) is modeled by: P(c)=-20(c-3)^2+180P(c)=−20(c−3) 2 +180

Answer 1

The current that produces maximum power is 3A

Explanation:

Given

`P(c) = 20(c - 3)^2`

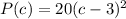
Required [Missing from the question]

The current that produces maximum power

First, we represent the function in standard form

`P(c) = 20(c - 3)^2`

`P(c) = 20(c - 3)(c - 3)`

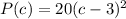
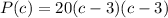
Open bracket

`P(c) = 20(c^2 -6c+ 9)`

`P(c) = 20c^2 -120c+ 180`

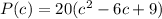
The maximum value of c is:

`Max(c) = (-b)/(2a)`

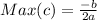
Where:

`f(x) = ax^2 + b^2 + c`

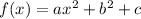
By comparison:
`P(c) = 20c^2 -120c+ 180`

`a = 20`

`b = -120`

`c = 180`

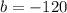
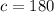
So, we have:

`Max(c) = (-b)/(2a)`

`Max(c) = (-(-120))/(2 * 20)`

`Max(c) = (120)/(40)`

`Max(c) = 3`