Question

A very long cylindrical shell made of copper has an inner radius 2 cm and an outer radius of 3 cm. This shell concentrically surrounds a very long charged aluminum rod of radius 1 cm with a charge density of 4 pC/m. All charges on the aluminum rod reside at its surface. The inner surface of the copper shell has exactly opposite charge to that of the aluminum rod while the outer surface of the copper shell has the same charge as the aluminum rod. Find the magnitude and direction of the electric field at points that are at the following distances from the center of the aluminum rod:

Answer 1

Question:

Find the magnitude and direction of the electric field at points that are at the following distances from the center of the aluminum rod:

(a) 0.5 cm, (b) 1.5 cm, (c) 2.5 cm, (d) 3.5 cm, (e) 7.0 cm

Answer:

(a) 0

(b) 4.795 N/C

(c) 2.877 N/C

(d) 2.055 N/C

(e) 1.027 N/C

Step-by-step explanation:

The given parameters are;

The inner radius of the copper = 2 cm

The outer radius of the copper - 3 cm

The radius of the aluminum rod, r = 1 cm

The radius of the aluminum rod = 4 pC/m

a) The charge at the 0.5 cm from the center of the aluminum rod, E = 0

There is no charge inside the rod given that the aluminum road is a conductor of electricity, having all the charge on its surface

b) At 1.5 cm, we have;

`E = (2 \cdot \lambda)/(4 \cdot \pi \cdot r \cdot \epsilon_0)`

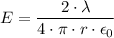
Where;

`( \lambda)/(4 \cdot \pi \cdot \epsilon_0) = 8.99 * 10^9 * 4 * 10^(-12)`

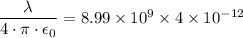
r = 1.5 cm = 0.015 m

∴ E = (2 × 8.99 × 10⁹ × 4 × 10⁻¹²)/0.015 ≈ 4.795

The magnitude of the electric field, E = 4.795 N/C

The direction of the charge depends on the charge sign on the rod

c) At 2.5 cm, we have;

r = 2.5 cm = 0.025 m

E = (2 × 8.99 × 10⁹ × 4 × 10⁻¹²)/0.025 ≈ 2.877

The magnitude of the electric field, E ≈ 2.877 N/C

d) At r = 3.5 cm, we have;

r = 3.5 cm = 0.035 m

E = (2 × 8.99 × 10⁹ × 4 × 10⁻¹²)/0.035 ≈ 2.055

The magnitude of the electric field, E ≈ 2.055 N/C

e) At

r = 7.0 cm = 0.070 m

E = (2 × 8.99 × 10⁹ × 4 × 10⁻¹²)/0.07 ≈ 1.027

The magnitude of the electric field, E ≈ 1.027 N/C