Question

A record is spinning on a turntable. A record is a uniform disk of mass 1.00 kg and a radius of 0.13 m that spins around an axis through its center. The record is initially spinning at 10 rad/s. Then the motor is turned off and the record slows to a stop with constant angular acceleration. As the record is slowing down it spins through 6.37 revolutions. What is the magnitude of the net torque acting on the record as it slows down

Answer 1

T = 0.01 Nm

Step-by-step explanation:

First, we will calculate the angular acceleration of the disk:

`2\theta\alpha = \omega_f^2-\omega_i^2`

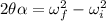
where,

θ = angular displacement = (6.37 rev)(2π rad/1 rev) = 40.02 rad/s

α = angular acceleration = ?

ωi = initial angular speed = 10 rad/s

ωf = final angular speed = 0 rad/s

Therefore,

`(2)(40.02\ rad/s)\alpha = (0\ rad/s)^2-(10\ rad/s)^2`

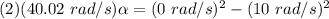
α = -1.25 rad/s²

negative sign shows deceleration

α = 1.25 rad/s²

Now, we will calculate the moment of inertia of disk:

`I = (1)/(2)mr^2`

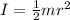
where,

I = Moment of Inertia = ?

m = mass of disk = 1 kg

r = radius of disk = 0.13 m

Therefore,

`I = (1)/(2) (1\ kg)(0.13\ m)^2`

I = 0.00845 kg.m²

Now, the torque can be given as:

T = Iα

T = (0.00845 kg.m²)(1.25 rad/s²)

T = 0.01 Nm